Az alapozások méretezéséről bölcsészeknek és teológushallgatóknak

Az épületek alapozása a kultúrmérnöki tudomány külön szakága. Könyvek százait írták tele az elméleti és gyakorlati tudnivalókkal. Az építkezőknek, de a régi házak tulajdonosainak is érdemes kicsit részletesebben megismerni e témát  - még akkor is, ha háza több évtizede, esetleg évszázada áll már a helyén. Ugyanis sok esetben az alapok kismértékű, rejtett sérüléseiből eredhetnek olyan problémák, melyek később már komolyabb beavatkozást igényelnek. És biztos vannak, akik bővíteni, felújítani szeretnék az épületüket, vagy el szeretnék végezni a szükséges fenntartási munkákat - ez a fejezet nekik is szól.

Elődeink mindenféle bonyolult számítás, hókusz-pókusz nélkül képesek voltak elkészíteni házaik alapozását. Az az igazság, hogy egészen a XIX. század közepéig – azaz a nagy tömegű városi építkezések megjelenéséig – nem sokat törődtek az alapozás előzetes méretezésével. Ez különösen igaz a köznép építkezésére, a lakóházak építésére. Azt tartották, hogy az olyan alap a jó, amelyik vaskos, széles – mert az ilyen mindenképpen megtartja a felette álló épületet. Földszintes épülethez a fallal azonos szélességű alapot építettek, emeletes háznál az ökölszabály az volt, hogy az alapnak a fölszinti fal szélessége kétszeresének kell lennie. A vályogfalak alá azonban tudjuk, hogy nagyon sokáig nem készültek a mai értelemben vett alapok. Pedig ezek eleve vastagabbra készültek minden más falnál (50-60 centisek sem ritkák) – és mégis állnak a mai napig…

De mi az alapozás?

Az alapozás azt a célt szolgálja, hogy a falakról a talajra jutó terhelést megfelelő módon átadja (és elossza) a teherbíró talajon. A gyakorlatban két fő alapozási rendszer ismeretes: az úgynevezett síkalapozás és a mélyalapozás.

Lakóházaink legtöbbje alatt síkalapozási rendszert találunk. Ennek műszaki, gazdasági és munkaszervezési okai vannak.

Egy régi mesterem kedvenc szavajárása szerint „az első számú műszaki paraméter, a ’mennyibe kerül’…”

Tény, hogy a kisebb épületek építésekor a legfontosabb szempont az, hogy a másodlagos (segéd-) szerkezetek ne drágítsák meg az épület megvalósítását. S az alapok éppen ilyen részei a háznak. Egy földszintes – vagy legfeljebb tetőtérbeépítéses – lakóház alatt egy igazi mélyalap (szekrényalapozás vagy cölöpalapozás) elkészítése bizony ugyanannyiba kerülhet, mint magának a háznak a felhúzása. Bár sajnos előfordul ennek ellenkezője is. Számos helyen olyan rossz minőségű a talaj, hogy nem lehet másképp biztosítani az épület állékonyságát.

Ezzel szemben a síkalapozási rendszerek viszonylag olcsók: nem kell olyan mélyen kiszedni a talajt, kisebb épített szerkezetek kellenek hozzá, s ami legalább ennyire fontos: a síkalap építésénél sok mindent házilagosan is kivitelezhetünk. Ami a mélyalapozási eljárásokra nem mondható el. A síkalapok lényege, hogy az a felszínhez közeli teherbíró rétegre adja át a terheket. Legelterjedtebb típusai a pontalap, a lemezalap és a sávalap.

A XIX. század utolsó harmadától kezdve - elsősorban a városi építkezések sokasodásával és egy új, modern anyag, a beton használatának széleskörűvé válásával - az alapokat már nem találomra, sok évszázados gyakorlati tapasztalatok szerint építették, hanem pontos számításokat dolgoztak ki erre a célra.

Az alábbiakban vázlatosan ismertetem az alapok tervezésének menetét. Nem célom, hogy bárki ennek alapján próbálja meg megtervezni háza alapozását, de a módszer leírása hasznos lehet abban, hogy egy leendő ház igen fontos részéről képünk legyen – vagy, hogy egy már meglévő ház alapszerkezetét jobban megismerhessük.

Az alapok tervezése komoly tartószerkezeti feladat, azt csak képzett szakember (építész vagy statikus) végezheti.

(A szerző viszonya a modern mértékegységekhez)

Mielőtt a részletekbe belemerülnénk, mindenképpen meg kell jegyeznem valamit.

A modern építészet, a statika napjaikban – illetve helyesebben szólva kb. 50-60 éve – igen bonyolult számításokkal végzi el egy-egy épületszerkezet megtervezését.

Ennek része, hogy olyan mértékegységeket használnak a tervezők (újabban a tervező programok), melyekkel a hétköznapi ember nemigen tud mit kezdeni. Newtonok (rövidítva: N), Pascalok és megaPascalok (Pa, Mpa), milliméterek szerepelnek a vonatkozó szabványokban, tervezési előírásokban. Megmondom őszintén, sok-sok éves, sőt évtizedes építőiparban töltött gyakorlatom ellenére nekem is igencsak el kellene gondolkodnom, ha valaki hirtelen rákérdezne, mi egy megaPascal, vagy ha azt kérné, ugyan már mutassam meg neki az 1 Newton erőt…

Az alábbiakban ezért a jó öreg, hétköznapokban használatos – azaz a valamikor az általános iskola 7-8. osztályában tanult – mértékegységekkel mutatom be a házalapok méretezésének menetét. Egy kiló lisztet vagy egy négyzetcentiméternyi felületet magam elé tudok képzelni – a Pascalt, mint mértékegységet, bevallom, nem megy…

Az alapok (és általában minden más épületszerkezet) tervezése során a fő cél, hogy a létrehozandó szerkezet teljesítse a rá szabott követelményeket, és hogy emellett megvalósítható (értsd: kivitelezhető) legyen.

Az alapok fő feladata, hogy elviseljék a felettük lévő épületrészek súlyát, és azt úgy továbbítsák a talaj felé, hogy se a talajban, se az épületben (és annak környezetében) kár ne keletkezzen.

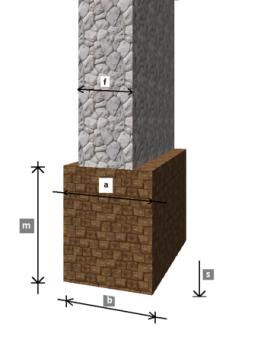
Ahhoz, hogy az alap e célnak megfeleljen és meg lehessen építeni, meg kell határozni méreteit, nagyságát.

Ezek:

ahol:   m = alaptest magassága

           f  = a fal szélessége

           a = alaptest felső síkjának szélessége

           b = alaptest alsó síkjának szélessége

           s = az alaptest alsó síkjának mélysége a felszíntől

Az épületszerkezetek tervezése két részből tevődik össze: a matematikai-statikai számításokból és a geometriai szerkesztésből.

A számítások eredményeként létrejövő szerkezetnek meg kell felelnie bizonyos szerkesztési szabályoknak is - ez főképp az alapoknál és felmenő falaknál lényeges elem.

Az alapok tervezésénél az alaptest alsó síkjának mélysége (azaz az alapozási sík szintje (s)) legtöbb esetben adott. Mégpedig ez a teherbíró talaj mélysége a felszín alatt.

Példánkban az egyszerűség kedvéért vegyük ezt 1,0 méternek.

Ahogy korábban már szó volt róla, az alap feladata a terhek elosztása a talaj felé. Mit jelent ez?

Minden talaj rendelkezik egy olyan teherbírással - a mérnöki nyelvben ezt törési határértéknek nevezzük (jele (s) szigma), melyet meghaladva a talaj roncsolódik, törik, azaz nem bírja tovább a terheket elviselni. Hogy megkülönböztessük a későbbi számítások eredményétől, nevezzük s_t –nek, azaz a talaj törési, tönkremeneteli határértékének. A kavicsos, homokos talajnál tömör állapotban ez a határérték nagyjából 7,5-7,8 kg/cm2, az agyagos talajnál 3,2-3,5 kg/cm2 (nedves állapotban mindkettő esetben a határérték kb. a felére csökken - ebből következik, hogy nem szabad olyan mélységig lemenni az alappal, ahol már nedves, vizes talaj található).

Amennyiben az épületszerkezetről ennél kisebb terhelés jut a talaj egy négyzetcentiméterére - nincs különösebb gond, már csak a szerkesztési elvekre kell ügyelni (ezekről később).

De nézzük csak, mekkora terhet jelent egy épületszerkezet (nevezetesen egy fal) a talajra.

Az egyszerűség kedvéért most egy sávalapot méretezünk. Ilyenkor úgy a legkönnyebb a számítás, ha egy 1 méteres szakasszal számolunk.

A fal szélessége adott: 0,5 méter.

Tehát a terhek.

Az épületek súlyát két fő tényező adja: a szerkezetek önsúlya és a használat során ehhez hozzáadódó súly. Könnyű belátni, hogy egy kőfalú háznál a terhelésben szerepet játszó fő tényező maga a szerkezet önsúlya.

A fal önsúlyát illetve az alap felé átadott súlyát, terhelését úgy számoljuk ki, hogy megszorozzuk a fal magasságát a térfogatsúlyával (fajsúlyával). Egy átlagos kőfal súlya valahol 1,9-2,5 tonna/m³ között van.

Az egyszerűség kedvéért számoljunk 2,0 tonna/m³-el. Azaz egy négyzetméternyi felületre egy 1 méter magas fal 2 tonna súllyal nehezedik.

Ha a fal 3 méter magas - egy átlagos földszintes lakóház falazata ennyi szokott lenni -, akkor az 3x2 tonna, azaz 6,0 tonna súlyt jelent négyzetméterenként.

Ehhez még hozzájönnek a használati és egyéb terhek - melyek igen sok összetevőből állnak (használati teher, a födém, a tető terhe, hóteher, dinamikus terhek stb. stb. ... ennek részletezése sok-sok oldalt tenne ki). Ám azt is tudjuk, hogy a kőfalak önsúlyához képest ezek a terhek nem olyan jelentősek, de azért számoljunk nagyjából 0,5 tonnával négyzetméterenként. A talajra jutó teher így 6,5 tonna négyzetméterenként. Amihez hozzájön még az alap önsúlya... De hát ezt honnan lehet tudni?

Bizony, először egy vázlatot kell készíteni, ami nagyjából meghatározza az alap méreteit. Ez kisebb házak egyszerű alapjainál 10 centiméteres pontosságot jelent, lehet, nagyobb épületeknél elég, ha 0,5-1,0 méteres becslés (egy tízemeletes ház alapjánál 0,5 méter vagy 1,0 méteres eltérés még nem olyan vészes a számítások kezdetekor. A végén úgyis pontos adatot kapunk majd...

Ha az alap 1 méter mély, akkor még annak súlya, azaz 2 tonna (térfogatsúly x szerkezeti magassággal) hozzájön az előző számhoz. Így összesen 8,5 tonna teherrel kell számolnunk.

Amikor eljutunk idáig, azaz megvan, hogy mennyi az összes teher, ezt még meg kell szoroznunk egy bizonyos, a szabványok, tervezési előírások által meghatározott biztonsági szorzóval... Ennek legyen az értéke most 1,5.

(A tartószerkezeti számítások Jolly Jokeréről, a biztonsági szorzóról)

Az önsúlyterhek, a használati és egyéb terhek számításánál - és minden más statikai számításnál - az előírások szerint mindenféle ("c", "k", "d", "n" betűkkel jelzett) biztonsági szorzók használatát írják elő.

 Károllyal, idős statikus tervező-szakértő kollégámmal szoktunk jókat mosolyogni az ilyen számítások ellenőrzésénél: a statikus, a tervező minden esetben hosszú-hosszú oldalakon át számolja ki a tartószerkezetek mutatóit, végső számait ... majd minden számítás végén szerepel egy 1-es, 2-es,  6-os, vagy 1,5-ös biztonsági együttható, ami tulajdonképpen az összes előző számítást feleslegesé teszi, felülírja...

Ezeknek a biztonsági tényezőket más statikus generációk hosszasan munkálták ki - de mire a felhasználásra érettek lettek, csak egy szerű 1-es, 2-es, 6-os vagy éppen 0,5-ös számmá fajultak. Lehetnének éppen 0,9, 2,2 vagy 6,5 is...

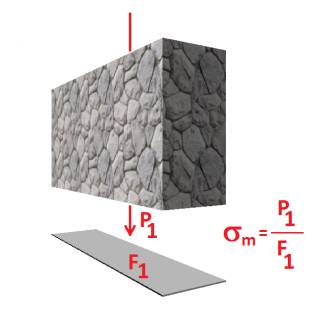
Végül eljutottunk oda, hogy megvan az a teher, ami a talajt nyomja: 8,5 tonna/m³ x 1,5 = azaz 12,75 tonna/m². Azaz 12750 kg/m³. Fél méter széles fal esetében egy 1,0 méteres falszakasz 6,375 tonna súlyt jelent. Azaz 6375 kg/5000 cm2 vagyis 1,275 kg jut 1 cm2-re.

Ezt nevezzük terhelésnek, vagy régi jelöléssel s (szigma).

Ez a szám még mindig változik egy kicsit - az alap elhelyezkedésének, alakjának, anyagának függvényében még újabb c1,c2,c3 biztonsági mutatókkal kell felszoroznunk a terhelést. A régi előírások szerint különféle mutatók összesen 3-as szorzót tehettek ki.

Vegyük ezt a legszélső esetnek. 1,275 x 3= 3.825 kg/ cm2.

Ez a szám a mértékadó terhelés, azaz s_m.

A bal oldali rajzon bejelöltem azt a felületet (F1), ahol megjelenik ez a terhelés (jelöljük P1-vel).

A példánkban agyagos talajjal számolva a talaj teherbírása (s_t) legyen 3,2 kg/ cm2.

E két adat ismeretében már egyszerűen kiszámolhatjuk az alap szélességét: a talaj felé akkor jut elviselhető terhelés, ha az alap olyan széles, hogy a fenti teher alatt nem megy tönkre.

Matematikailag: az alap akkor elég széles, ha a s_m < s_t azaz a mértékadó terhelés kisebb, mint a talaj törési, tönkremeneteli határértéke.

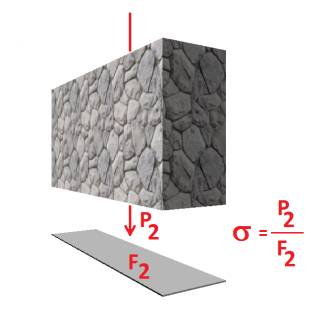
Hogy ez megvalósuljon, vagy csökkentem a terhet, vagy meg kell növelni azt a felületet, amelyen a teher átadódik a talaj felé. Ezt a terhelést a jobb oldali rajzon P2-vel jelöltem, a felületet, ahol ez átadódik: F2-vel. Mivel a hossz adott (1 méter) a szélességet növelhetem.

Ha a szélességet 50 centi helyett mondjuk 60 centivel számítjuk, akkor az egy négyzetcentiméterre eső terhelés (falhossz 1 méter):

6375 kg/ 6000 cm2 = 1,0625 kg/ cm2

Biztonsági szorzóval: 1.0625 x 3 = 3.1825 kg/cm2, ami már kisebb, mint 3,2 kg/ cm2.

Ugyanez a másik irányból számolva: ha nekem 3,2 kg/ cm2-nél kisebb terhelést kell előállítanom, akkor a legkisebb szélességnek az alábbi számítással adódik:

6375 kg (súly) osztva 3,2 kg/ cm2 (határfeszültség) szorozva 3 (biztonsági szorzó)

100 cm (falhossz)

azaz 59,76 cm, vagyis felfelé kerekítve 60 cm.

 (a tartószerkezeti számításoknál mindig felfelé kerekítünk egész számra)

Ellenőrzés:

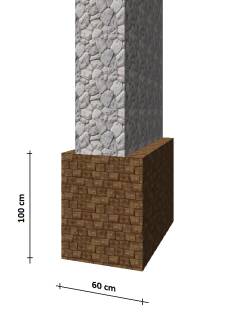
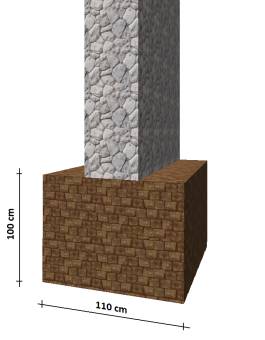
6375 kg / 6000 cm2 x 3 = 3.1825 kg/ cm2 ami kisebb mint 3.2 kg/ cm2

 (100 x 60 cm = 6000 cm2)

Az alapunk tehát így néz ki:

Az alapok tervezésének második lépcsője, hogy a szerkesztési előírásokat is teljesítenünk kell.

-   az alapnak legalább 50 centi magasnak kell lennie - ez teljesül.

-   az alap felső szélének a legalább 5-5 centivel szélesebbnek kell lennie, mint a fal síkjának - ez is teljesül

Azaz az alapunk megfelel az előírásoknak...

Hogy a további előírásokat is megértsük, vegyük azt az esetet, amikor az épületünk nem egy szintes, hanem mondjuk kettő... Ebben az esetben a terhelés egy méter hosszú alap esetében már legalább kétszer akkora, hisz a fal kétszer olyan magas.

Azaz a fal önsúlya 12 tonna. A hasznos és egyéb terhek is megnőnek valamennyit - hisz két szintet alakítunk ki. A növekedés legyen 1 tonna - ez így együtt 13 tonna. Az alap magassági mérete maradjon egy méter - ez újabb két tonnát jelent, azaz összesen 15 tonna a talajra adódó teher.

A biztonsági szorzót vegyük ismét 1,5-szörösre. Így a mértékadó terhelésünk 22,5 tonna, egy folyóméter hosszú és fél méter széles fal esetében (22,5 x 0,5) = 11,25 tonna. 11250 kg/5000 cm-el: 2,25 kg/ cm2.

3-as biztonsági szorzóval a mértékadó terhelés: 6,75 kg/ cm2.

A fenti számítások megismétlésével az alap szélessége:

11250 kg (súly) osztva 3,2 kg/ cm2 (határfeszültség) szorozva 3 (biztonsági szorzó)

100 cm (falhossz)

azaz 105,46 cm, vagyis 110 cm.

Ellenőrzés:

11250 kg / 11000 cm2 x 3 = 3.068 kg/cm2 ami kisebb, mint 3.2 kg/cm2

(100 x 110 cm= 11000 cm2)

Ez az alap így nézne ki:

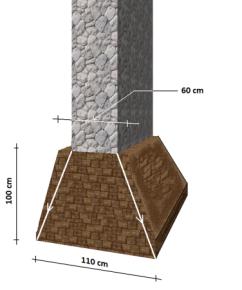
Igen ám, de az ilyen alap egyrészt igen sok anyagot igényel (melyek egy része feleslegesen kerülne beépítésre, mert nem hord terhet), és más problémák is fellépnek (nyírási erő a jelölt helyen). Ezért elővesszük újra a szerkesztési szabályokat, amelyek kimondják, hogy bizonyos méretű alapnál szélesítést kell alkalmazni lefelé, azaz az alap trapéz keresztmetszetű legyen.

Fent tehát elég, ha 5 centivel szélesebb az alap, mint a fal. Lent 110 centi széles lesz. Így fog kinézni:

Betonalapoknál ez a forma megalkotható. Kő és téglalapoknál ezzel szemben megengedett a lépcsőzés kialakítása, mégpedig ilyen formában:

A lépcsőzést úgy kell kialakítani, hogy ne nyúljon bele abba a ferde vonalba, mely tulajdonképpen a teherátadás szélső határát adja ki. Mit jelent ez tégla és kőfalaknál? Azt, hogy a téglák, kövek kijjebb kell, hogy ugorjanak, mint ezt a teherátadási vonal. Azaz így nézhet ki a kőalap:

A téglaalapoknál a lépcsőzés legalább fél tégla vastagágú kell, hogy legyen. Kőalapoknál viszont az a fontos, hogy a szélső kövek mindenhol úgy kössenek be az alaptömbbe, hogy keresztezzék, azaz metsszék ezt a terhelési vonalat - hézag nem eshet a terhelési hatásvonalba. És természetesen felesleges e vonalon kívül kövek beépítése - mert ezek már nem játszanak szerepet a teherviselésben.

És ezzel a végére értünk a számításnak. Az alap méretei nagyjából rendelkezésre állanak. Hátradőlhetünk… és felkereshetjük statikus, építész ismerősünket, hogy akkor most már ő is tervezze meg a házunkat, alapjaival együtt. Természetesen a mai modern szakemberek már számítógéppel dolgoznak…  lefuttatják a programot, és meglepődve tapasztaljuk, hogy a leendő házunk alapjának valóban 60 vagy éppen 110 cm szélesnek kell lennie… bocsánat, 600 mm-esnek vagy 1100 mm-esnek…

A fentiek alapján - ha megtervezni nem is tudjuk - de legalább nagyjából lesz fogalmunk az alapok méretezéséről.